

최단거리 알고리즘
Series
정리 안해두면 까먹을거 같아서 기억력을 조금이라도 향상시키기 위해 정리해둔다.
자, 최단거리 알고리즘을 이해하기 위해 그래프를 간략히 살펴보면
그래프란?
그래프는 정점(Vertex) 와 간선(Edge) 을 모아놓은 자료구조다.
그래프라는 친구는 보통 간선에 가중치를 가진다.
구현 방법
- 인접 행렬
- 인접 리스트
다익스트라 알고리즘
최단 거리 알고리즘은 기본적으로 그리디 알고리즘 으로 분류된다.
-> 매번 가장 비용이 적은 노드 를 선택하는 과정을 반복하기 때문이다.
전제조건
- 시작 노드 - 시작 노드 사이 거리는 0이다.
- 모든 간선은 양의 가중치를 가진다.
특징
- 구현 방법은 2가지
1. 직관적인 방법 - O(V^2)
- 각 노드에 대한 최단 거리를 담는 1차원 리스트 선언
- 방문하지 않은 노드 중에서 거리가 가장 짧은 노드 선택
(거리가 같으면 일반적으로 번호가 작은 노드) - 거리가 더 짧으면 값 갱신
최단거리 - 백준 1753

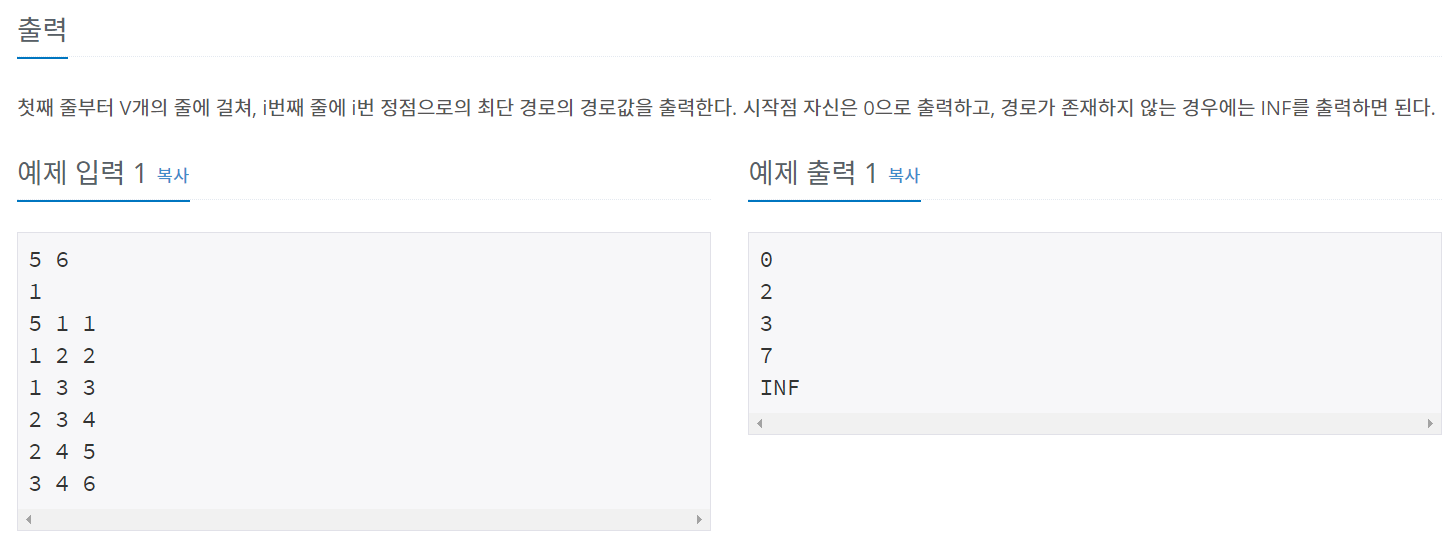
package package24;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
public class num1753 {
static int INF = Integer.MAX_VALUE;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] inputVE = br.readLine().split(" ");
int V = stoi(inputVE[0]);
int E = stoi(inputVE[1]);
int K = stoi(br.readLine())-1;
List<Edge>[] graph = new ArrayList[V];
for (int i = 0; i < V; i++)
graph[i] = new ArrayList<>();
int[] distance = new int[V];
boolean[] visited = new boolean[V];
for(int i=0; i<V; i++) {
distance[i] = INF;
}
for(int i=0; i<E; i++) {
String[] uvw = br.readLine().split(" ");
int u = stoi(uvw[0])-1;
int v = stoi(uvw[1])-1;
int w = stoi(uvw[2]);
graph[u].add(new Edge(v,w));
}
dijkstra(graph, visited, distance, V, E, K);
for(int value : distance) {
if(INF == value)
System.out.println("INF");
else
System.out.println(value);
}
}
public static void dijkstra(List<Edge>[] graph, boolean[] visited, int[] distance, int V, int E, int K) {
distance[K] = 0;
for(int i=0; i<V; i++) {
int minIndex = getSmallestNodeNotVisited(visited, distance, V);
for (Edge next : graph[minIndex]) {
if(!visited[next.v] && distance[next.v] > distance[minIndex] + next.weight) {
distance[next.v] = distance[minIndex] + next.weight;
}
}
visited[minIndex] = true;
}
}
public static int getSmallestNodeNotVisited(boolean[] visited, int[] distance, int V) {
int min = INF;
int minIndex = 0;
for(int i=0; i<V; i++) {
if(visited[i] == false && distance[i]<min) {
min = distance[i];
minIndex = i;
}
}
return minIndex;
}
public static int stoi(String string) {
return Integer.parseInt(string);
}
}
class Edge {
int v, weight;
public Edge(int v, int weight) {
this.v = v;
this.weight = weight;
}
}
소스를 간략히 설명하면
노드 arrayList를 만들고 Edge는 클래스로 만들어서 넣어주는 방법으로 구현했다.
(배열로만 구현하면 메모리 초과난다.)
매번 최단거리가 가장 짧은 노드를 찾기 위해 O(V) 만큼 탐색하기 때문에 비효율적이다.
-> Priority Queue 활용
2. Priority Queue 활용 - O(ElogV)
최단 거리 -> 최소 힙을 사용한다.
1. 각 노드에 대한 최단 거리를 담는 1차원 리스트 선언
2. 우선순위 큐을 사용해 거리가 짧은 정점부터 Queue에 넣어 줌.(처음 시작 값 : 0)
3. 큐가 값이 없을 때까지 반복
3-1) 큐에서 값을 하나 꺼냄 (Vertex 선택)
3-2) visited 값 true 설정
4. 다음 Vertex의 최단거리가 현재Vertex 최단 거리 + 다음 Vertex 가중치보다 크면
(다음 Vertex가 사용되지 않았을 때)
4-1) 값 갱신
4-2) 우선순위 큐에 값 추가요약하면
1. 아직 방문하지 않은 정점 중 거리가 짧은 정점을 하나 선택해 방문
2. 해당 정점에 인접하고 아직 방문하지 않은 정점의 최단거리 갱신Tip!!
JAVA PriorityQueue 는 기본적으로 minHeap이다.
// 최소 힙
PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>();
// 최대 힙
PriorityQueue<Integer> maxHeap = new PriorityQueue<Integer>(Comparator.reverseOrder());
// 최대 힙 version2
PriorityQueue<Integer> maxHeap = PriorityQueue<>(new Comparator<Integer>(){
@Override
public int compare(Integer i1, Integer i2) {
return i2-i1;
}
});최단거리 - 백준 1504
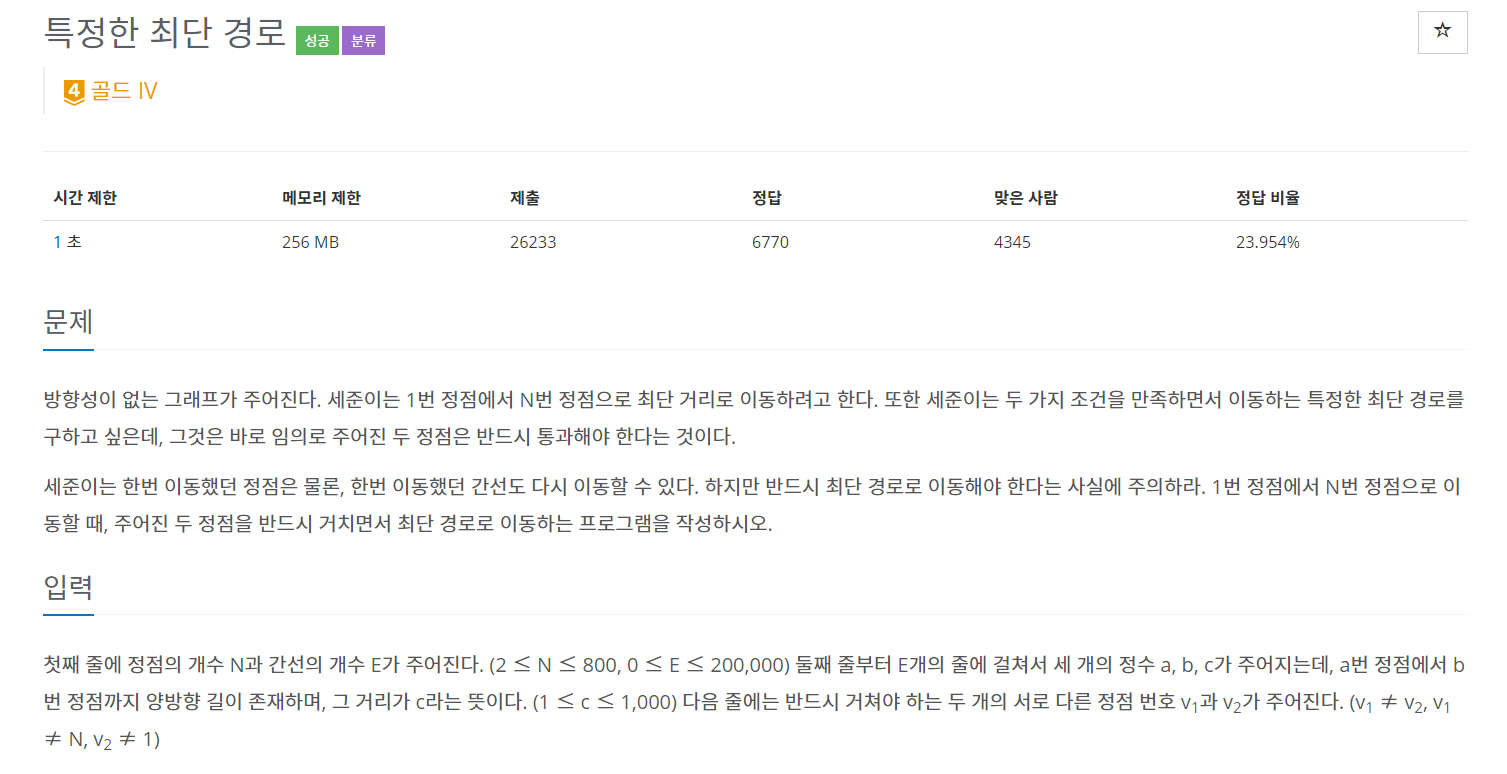
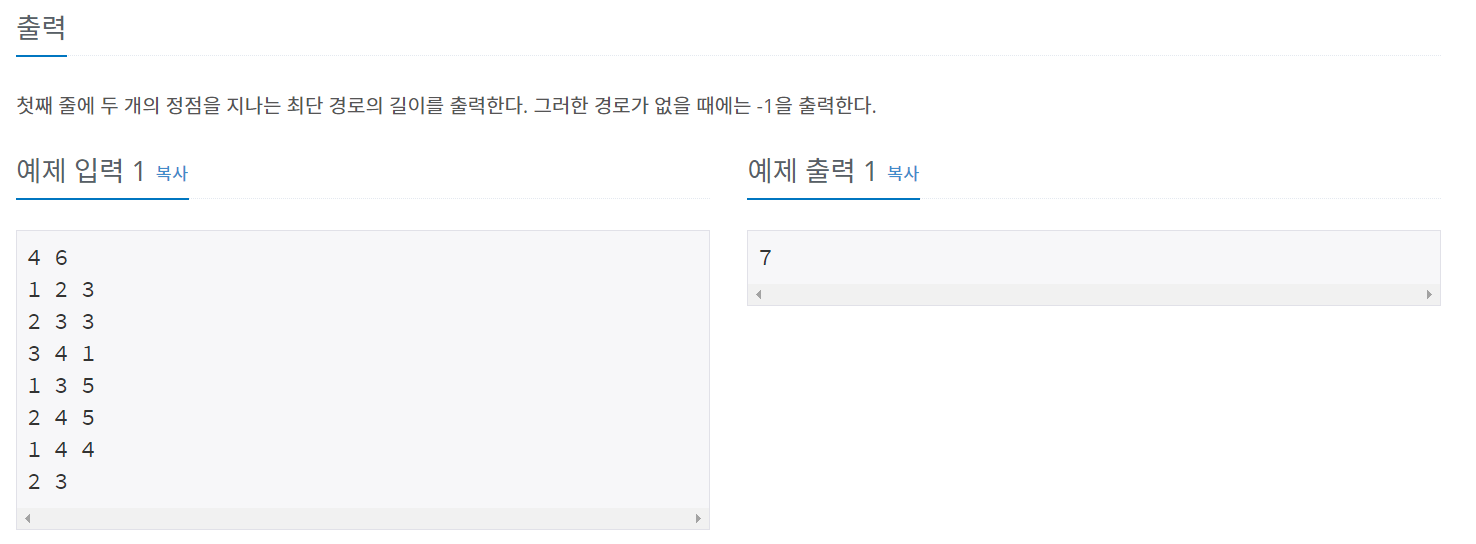
문제를 보면 정점 2개를 방문해야 한다는 조건이 있다. 정점을 각각 V1, V2라고 한다면
- 1 -> V1 -> V2 -> N
- 1 -> V2 -> V1 -> N
두가지 경우에 대해 구간별로 최소값을 구한 후, 더하면 된다.
package package24;
import java.io.*;
import java.util.*;
public class num1504 {
static int N,E,v1,v2,result;
static ArrayList<ArrayList<Edge>> Vertex;
static int[] distance;
static boolean[] visited;
static int INF = 200000000;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] NE = br.readLine().split(" ");
N = stoi(NE[0]);
E = stoi(NE[1]);
distance = new int[N+1];
visited = new boolean[N+1];
Vertex = new ArrayList<>();
for(int i=0; i<=N; i++) {
Vertex.add(new ArrayList<>());
}
for(int i=0; i<E; i++) {
String[] abc = br.readLine().split(" ");
int a = stoi(abc[0]);
int b = stoi(abc[1]);
int c = stoi(abc[2]);
Vertex.get(a).add(new Edge(b,c));
Vertex.get(b).add(new Edge(a,c));
}
String[] v1v2 = br.readLine().split(" ");
v1 = stoi(v1v2[0]);
v2 = stoi(v1v2[1]);
result = solve();
System.out.println(result);
}
public static int solve() {
int case1=0, case2=0;
case1 = dijkstra(1,v1) + dijkstra(v1,v2) + dijkstra(v2,N);
case2 = dijkstra(1,v2) + dijkstra(v2,v1) + dijkstra(v1,N);
return (case1 >= INF && case2 >= INF) ? -1 : Math.min(case1, case2);
}
public static int dijkstra(int start, int end) {
Arrays.fill(distance, INF);
Arrays.fill(visited, false);
PriorityQueue<Edge> queue = new PriorityQueue<Edge>();
queue.add(new Edge(start,0));
distance[start] = 0;
while(!queue.isEmpty()) {
Edge now = queue.remove();
int nowNode = now.e;
if(!visited[nowNode]) {
visited[nowNode] = true;
for(Edge next : Vertex.get(nowNode)) {
if(!visited[next.e] && distance[next.e] > distance[nowNode] + next.weight) {
distance[next.e] = distance[nowNode] + next.weight;
queue.add(new Edge(next.e, distance[next.e]));
}
}
}
}
return distance[end];
}
public static int stoi(String string) {
return Integer.parseInt(string);
}
static class Edge implements Comparable<Edge>{
int e, weight;
Edge(int e, int weight){
this.e = e;
this.weight = weight;
}
@Override
public int compareTo(Edge o){
return weight - o.weight;
}
}
}벨만-포드 알고리즘
특징
- 시간 복잡도 - O(VE)
- 다익스트라 알고리즘보다 느리지만 음의 가중치를 가진 경로의 최단거리를 구할 수 있다.
전제 조건
- 같은 정점을 2번 지날일은 없기 때문에 간선의 최대 개수는 V-1이다.
- 음수 사이클이 없는 최단 경로를 구해야 한다.
존재하는 모든 간선을 돌아보면서 간선이 통할 수도 있는 거리를 갱신하는 것
백준 11657
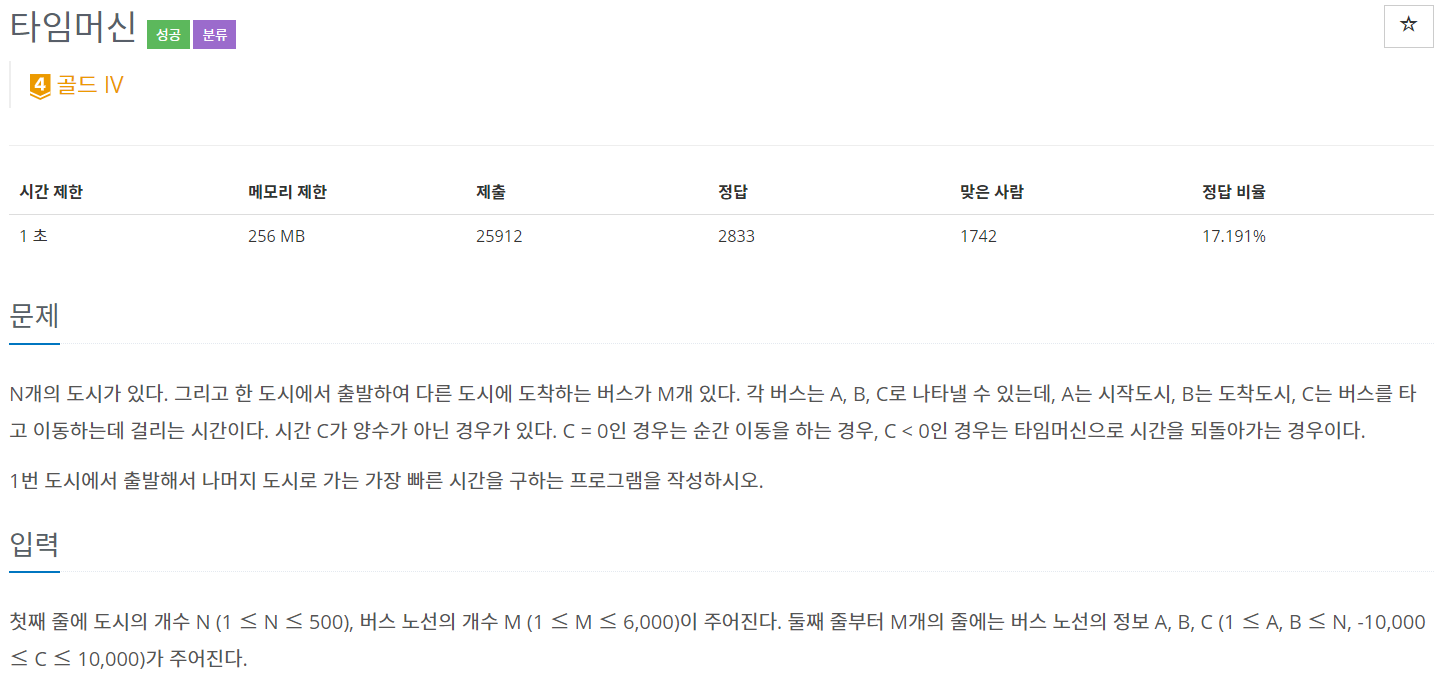
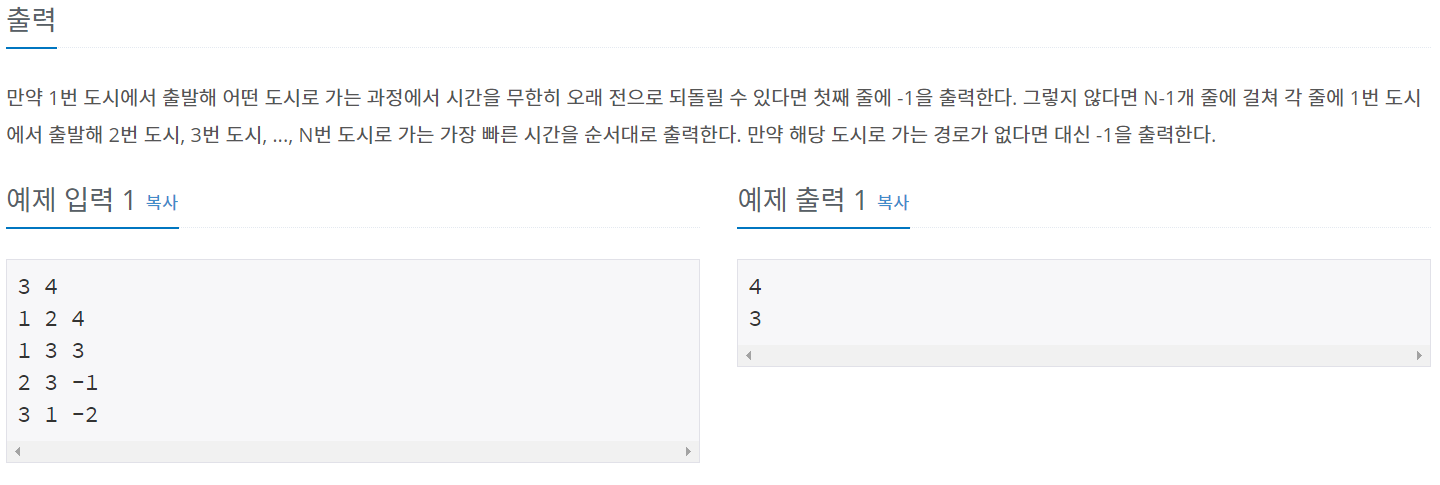
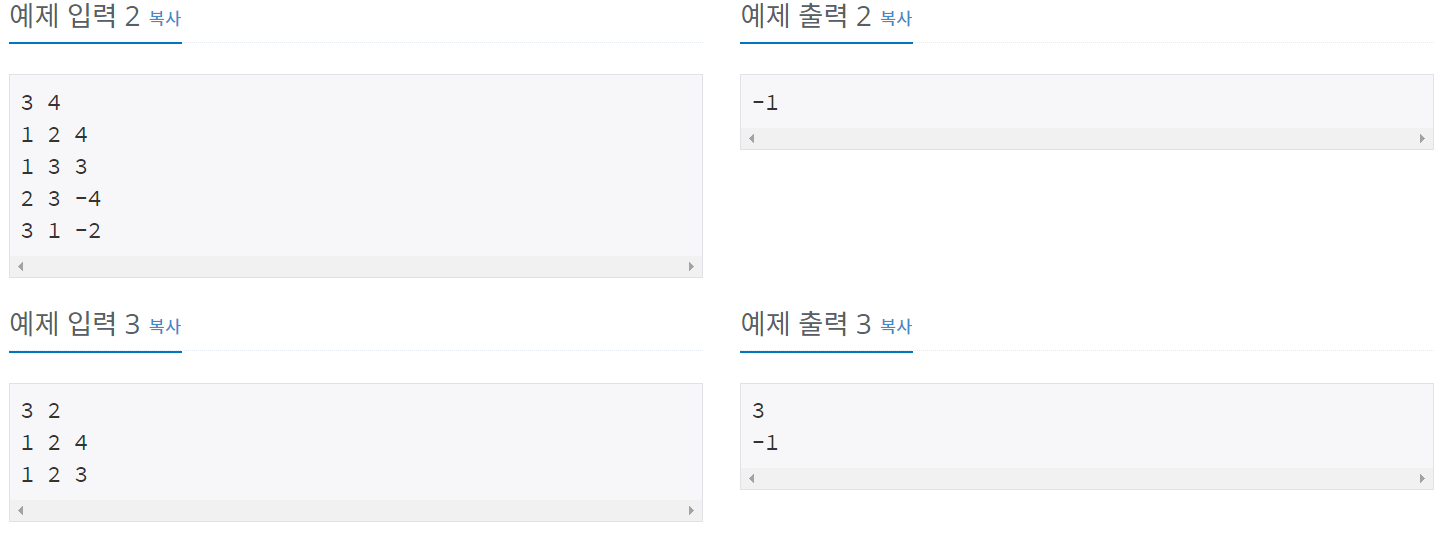
package package24;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
public class num11657 {
static int N, M;
static ArrayList<ArrayList<Edge>> Vertex;
static long[] dist;
static int INF = Integer.MAX_VALUE;
static boolean minusCycle=false;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
String[] inputNM = br.readLine().split(" ");
N = stoi(inputNM[0]);
M = stoi(inputNM[1]);
dist = new long[N];
Vertex = new ArrayList<ArrayList<Edge>>();
for(int i=0; i<N; i++) {
Vertex.add(new ArrayList<Edge>());
dist[i] = INF;
}
for(int i=0; i<M; i++) {
String[] ABC = br.readLine().split(" ");
int A = stoi(ABC[0])-1;
int B = stoi(ABC[1])-1;
int C = stoi(ABC[2]);
Vertex.get(A).add(new Edge(B,C));
}
bellman();
if(minusCycle)
sb.append("-1\n");
else {
for(int i=1; i<N; i++) {
sb.append(dist[i] != INF ? dist[i] : -1);
sb.append("\n");
}
}
System.out.println(sb.toString());
}
public static void bellman() {
dist[0] = 0;
for(int i=0; i<N; i++){
for(int j=0; j<N; j++){
for(Edge edge: Vertex.get(j)){
int next = edge.e, w = edge.w;
if(dist[j] != INF && dist[next] > dist[j] + w){
dist[next] = dist[j] + w;
if(i == N-1) minusCycle = true;
}
}
}
}
}
static class Edge {
int e, w;
Edge(int e, int w) {
this.e = e;
this.w = w;
}
}
public static int stoi(String string) {
return Integer.parseInt(string);
}
}코드를 간단히 설명해보면
존재하는 모든 간선을 돌아보면서 이 간선을 통할 수도 있는 최단경로들의 거리를 갱신한다. 같은 정점을 2번 방문하는 경우는 없다는 전제가 있으므로 V-1까지 확인한다 만약, 음의 사이클이 존재한다면 -> V-1 이후 최단거리가 갱신된다. 위의 소스에선 V까지 루프의 마지막에 최단거리가 갱신되는지 확인한다.
이 문제는 조금 주의할 점이 있다.
최소 가중치가 -10000이라 언더플로우가 생길 수 있기 때문에 dist를 long[]으로 설정해야 한다.
플로이드 알고리즘
특징
- 다익스트라, 벨만 포드 알고리즘 : 하나의 시작점에 대한 최단 거리
- 플로이드 워셜 알고리즘 : 모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야 하는 경우
- 시간 복잡도 : O(V^3)
-> 노드의 개수 O(V) * 현재 노드를 거쳐가는 모든 경로O(V^2) -> O(V^3) - DP형태 -> 점화식에 맞게 2차원 리스트를 갱신하기 때문
Tip!!
상황에 따라 자기 자신으로 이동 가능하면 dis[i][j] = 0 / 불가능하면 dis[i][j] = INF
- 가장 바깥쪽 for문은 경유할 정점
- 가운데 for문은 출발 정점
- 가장 안쪽 for문은 도착 정점
백준 11404
package package24;
import java.io.*;
public class num11404 {
static int N, M, INF = 100000000;
static int[][] dis;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringBuilder sb = new StringBuilder();
N = stoi(br.readLine());
M = stoi(br.readLine());
dis = new int[N][N];
for(int i=0; i<N; i++) {
for(int j=0; j<N; j++) {
dis[i][j] = i == j ? 0 : INF;
}
}
for(int i=0; i<M; i++) {
String[] abc = br.readLine().split(" ");
int a = stoi(abc[0])-1;
int b = stoi(abc[1])-1;
int c = stoi(abc[2]);
dis[a][b] = Math.min(dis[a][b], c);
}
for(int k=0; k<N; k++) {
for(int i=0; i<N; i++) {
for(int j=0; j<N; j++) {
dis[i][j] = Math.min(dis[i][j], dis[i][k] +dis[k][j]);
}
}
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
dis[i][j] = dis[i][j] == INF ? 0 : dis[i][j];
sb.append(dis[i][j] + " ");
}
sb.append("\n");
}
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
public static int stoi(String string) {
return Integer.parseInt(string);
}
}정리
이렇게 최단거리 알고리즘 3가지를 알아보았다.
사용하는 경우를 정리해보면
1. 다익스트라 알고리즘[우선순위 큐] -> 한 지점에서 다른 지점까지 최단거리 구하는 문제
2. 벨만 포드 알고리즘 -> 음의 가중치를 가진 최단거리 구하는 문제
3. 플로이드 와샬 알고리즘 -> 모든 경로의 최단거리 구하는 문제로 정리할 수 있다.
생각보다 어려워서 정리하는데 시간이 오래걸렸다.
다음 글은 최단경로의 경로출력에 대해 정리해 볼 예정이다.
추가로 라이님 블로그 요기 있는 추가문제 하나씩 풀어봐야겠다.
Reference
라이님 블로그
갓킹독님 블로그
Crocus님 블로그
백준 질문하기 - 출력초과 문제 해결이 되었는데 이유를 모르겠습니다
이것이 코딩테스트다 - 나동빈