백준 단계별 문제 - 투포인터에 있는 1644번 문제를 풀다 소수 구하는 알고리즘이 생각이 안나서 정리 해둘 겸 포스팅한다.

에라토스테네스의 체란?

소수가 되는 수의 배수를 지우면 남는 건 소수가 된다

요런 알고리즘이다.

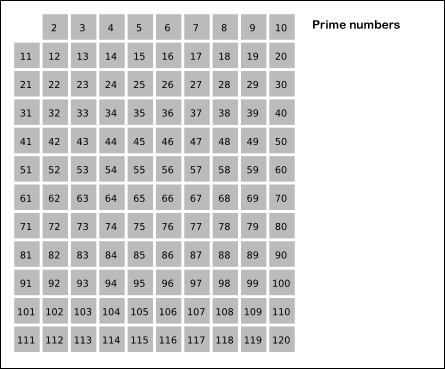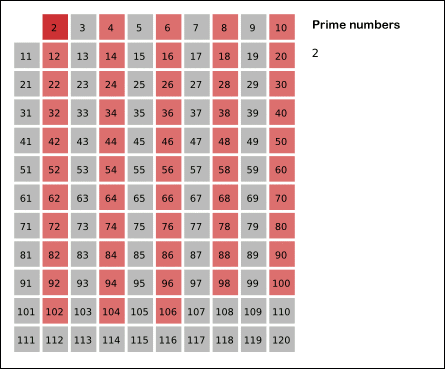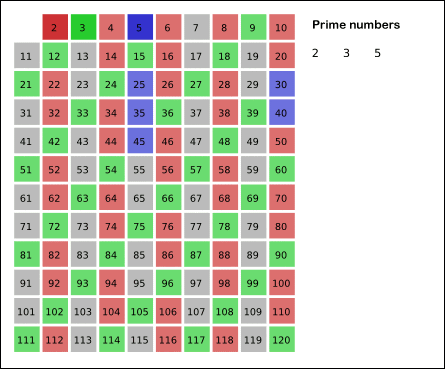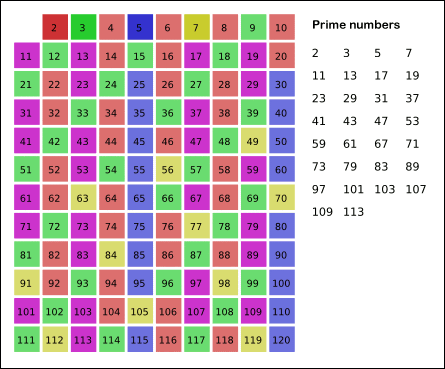
백준 1644 - 소수의 연속 합

1. 에라토스테네스의 체로 소수 구하는 방법을 활용해 소수를 구한다.
2. 투포인터 알고리즘을 활용해 연속 합 확인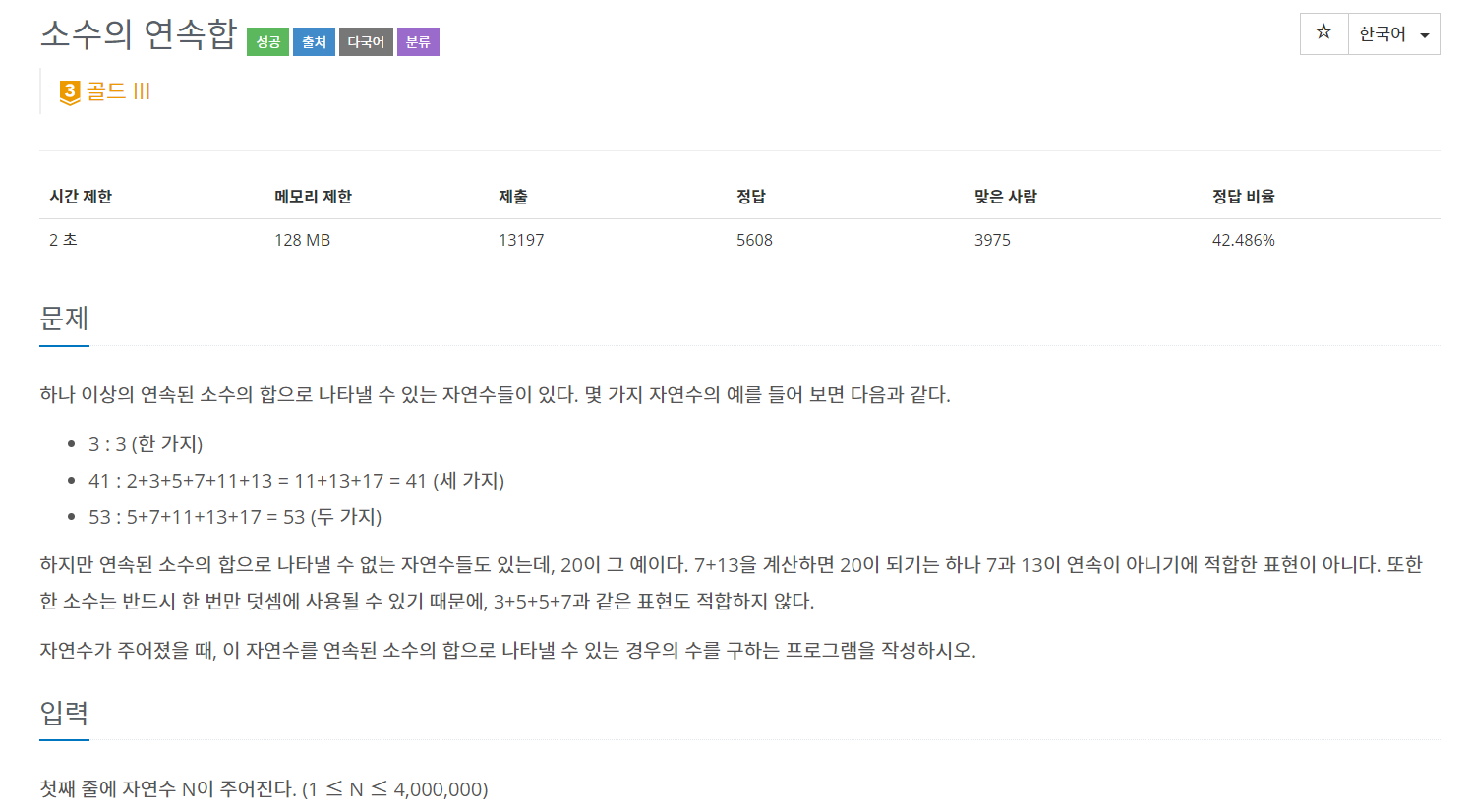

package package25;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;

public class num1644 {
	static int N, sum = 0, s = 0, e = 0, count = 0;
	static boolean primeCheckArr[];
	static ArrayList<Integer> primeList;

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

		N = stoi(br.readLine());
		primeCheckArr = new boolean[N+1];
        primeList = new ArrayList<Integer>();

        getPrimeNumber();

        getCountResult();

        System.out.println(count);

	}

	public static void getCountResult() {
		while(true) {
			if(sum>=N) sum-=primeList.get(s++);
			else if(e == primeList.size()) break;
			else sum+=primeList.get(e++);
			if(sum == N) count++;
		}
	}

	public static void getPrimeNumber() {
		primeCheckArr[0] = primeCheckArr[1] = true;

        for(int i=2; i*i<=N; i++){
            if(!primeCheckArr[i]) {
            	for(int j=i*i; j<=N; j+=i)
            		primeCheckArr[j]=true;
            }
        }

        for(int i=1; i<=N;i++){
        	if(!primeCheckArr[i]) primeList.add(i);
        }
	}

	public static int stoi(String string) {
		return Integer.parseInt(string);
	}

}

추가로 소수를 구하는 부분의 for문을 살펴보면

for(int i=2; i*i<=N; i++){
    if(!primeCheckArr[i]) {
    	for(int j=i*i; j<=N; j+=i)
    		primeCheckArr[j]=true;
    }
}

특정한 소수의 제곱근 까지만 구하면 된다 -> 약수가 아닌경우는 수가 대칭을 이루기 때문

Reference

위키 백과