Ian's Archive 🏃🏻

순열, 조합, 중복 순열, 중복 조합, 부분 집합

Algorithm

2022.10.31.

n, m, arr을 받아 순열, 조합, 중복 순열, 중복 조합 전부 출력하는 형태로 구현 해보자

정리하고 백트래킹 문제 좀 풀어봐야 겠따

종류	정의	중복	순서
순열	n개의 원소 중 r개를 순서를 고려 해 나열	X	O
중복 순열	n개의 원소 중 r개를 중복을 허용하고, 순서 고려해 나열	O	O
조합	n개의 원소 중 r개를 순서 생각하지 않고 나열	X	X
중복 조합	n개의 원소 중 r개를 중복을 허용하고, 순서를 생각하지 않고	O	X

순열

copyButtonText

    // static int arr[], n, r, totalCnt / ArrayList<int[]> res; / boolean[] visited
    public static void permutation(int cnt, int[] selected) {
        if (cnt == r) {
            totalCnt++;

            int[] saveArr = selected.clone();
            res.add(saveArr);

            return;
        }

        for (int i = 0; i < n; i++) {
            if (visited[i]) {
                continue;
            }

            visited[i] = true;
            selected[cnt] = arr[i];
            permutation(cnt + 1, selected);
            visited[i] = false;
        }
    }

visited배열을 사용해서 방문체크를 해 중복 제거하며 전체를 돌 수 있게 한다

중복 순열

copyButtonText

    // static int arr[], n, r, totalCnt / ArrayList<int[]> res; / boolean[] visited
    public static void rePermutation(int cnt, int[] selected) {
        if (cnt == r) {
            totalCnt++;

            int[] saveArr = selected.clone();
            res.add(saveArr);

            return;
        }

        for (int i = 0; i < n; i++) {
            selected[cnt] = arr[i];
            rePermutation(cnt + 1, selected);
        }
    }

순열에서 중복 된 값을 처리해주는 visited 배열 제거

조합

copyButtonText

    // static int arr[], n, r, totalCnt / ArrayList<int[]> res;
    public static void combination(int idx, int cnt, int[] selected) {
        if(cnt == r) {
            totalCnt++;

            int[] saveArr = selected.clone(); // 객체 복사 - 원본 배열과 별개의 주소값으로 새로운 객체 생성
            res.add(saveArr);

            return;
        }

        for(int i = idx; i<n; i++){
            selected[cnt] = arr[i];
            combination(i + 1, cnt + 1, selected);
        }
    }

index를 변경해 이전 수 참조할 수 없게 다음 값을 인덱스로 전달

중복 조합

copyButtonText

    // static int arr[], n, r, totalCnt / ArrayList<int[]> res;
    public static void reCombination(int idx, int cnt, int[] selected) {
        if (cnt == r) {
            totalCnt++;

            int[] saveArr = selected.clone(); // 객체 복사 - 원본 배열과 별개의 주소값으로 새로운 객체 생성
            res.add(saveArr);

            return;
        }

        for (int i = idx; i < n; i++) {
            selected[cnt] = arr[i];
            reCombination(i, cnt + 1, selected);
        }
    }s

중복 조합은 조합 소스에서 index를 자기 자신은 가능하지만, 이전 값들을 다시 쓸 수 없게 구현하면 된다.

전체 소스

copyButtonText

package math;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;

public class example {
    static int arr[], n, r, totalCnt;
    static boolean visited[];
    static ArrayList<int[]> res;

    static String[] commands = {
            "permutation", "rePermutation", "combination", "reCombination"
    };

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] nr = br.readLine().split(" ");

        n = stoi(nr[0]);
        r = stoi(nr[1]);
        arr = new int[n];

        String[] input = br.readLine().split(" ");
        for (int i = 0; i < n; i++) {
            arr[i] = stoi(input[i]);
        }

        for (String command : commands) {
            run(command);
        }
    }

    public static void run(String command) {
        init();

        switch (command) {
            case "permutation":
                permutation(0, new int[r]);
                break;
            case "rePermutation":
                rePermutation(0, new int[r]);
                break;
            case "combination":
                combination(0, 0, new int[r]);
                break;
            case "reCombination":
                reCombination(0, 0, new int[r]);
                break;
        }

        printResult(command);
    }

    public static void init() {
        totalCnt = 0;
        res = new ArrayList<>();
        visited = new boolean[n];
    }

    // static int arr[], n, r, totalCnt / ArrayList<int[]> res; / boolean[] visited
    public static void permutation(int cnt, int[] selected) {
        if (cnt == r) {
            totalCnt++;

            int[] saveArr = selected.clone();
            res.add(saveArr);

            return;
        }

        for (int i = 0; i < n; i++) {
            if (visited[i]) {
                continue;
            }

            visited[i] = true;
            selected[cnt] = arr[i];
            permutation(cnt + 1, selected);
            visited[i] = false;
        }
    }

    // static int arr[], n, r, totalCnt / ArrayList<int[]> res; / boolean[] visited
    public static void rePermutation(int cnt, int[] selected) {
        if (cnt == r) {
            totalCnt++;

            int[] saveArr = selected.clone();
            res.add(saveArr);

            return;
        }

        for (int i = 0; i < n; i++) {
            selected[cnt] = arr[i];
            rePermutation(cnt + 1, selected);
        }
    }

    // static int arr[], n, r, totalCnt / ArrayList<int[]> res;
    public static void combination(int idx, int cnt, int[] selected) {
        if (cnt == r) {
            totalCnt++;

            int[] saveArr = selected.clone(); // 객체 복사 - 원본 배열과 별개의 주소값으로 새로운 객체 생성
            res.add(saveArr);

            return;
        }

        for (int i = idx; i < n; i++) {
            selected[cnt] = arr[i];
            combination(i + 1, cnt + 1, selected);
        }
    }

    // static int arr[], n, r, totalCnt / ArrayList<int[]> res;
    public static void reCombination(int idx, int cnt, int[] selected) {
        if (cnt == r) {
            totalCnt++;

            int[] saveArr = selected.clone(); // 객체 복사 - 원본 배열과 별개의 주소값으로 새로운 객체 생성
            res.add(saveArr);

            return;
        }

        for (int i = idx; i < n; i++) {
            selected[cnt] = arr[i];
            reCombination(i, cnt + 1, selected);
        }
    }

    public static void printResult(String command) {
        System.out.print(command);

        System.out.print("( ");
        for (int n : arr) {
            System.out.print(n + " ");
        }
        System.out.println(")");
        System.out.println("totalCount : " + totalCnt);

        for (int[] list : res) {
            for (int item : list) {
                System.out.print(item + " ");
            }
            System.out.println();
        }
        System.out.println();
    }

    public static int stoi(String s) {
        return Integer.parseInt(s);
    }
}

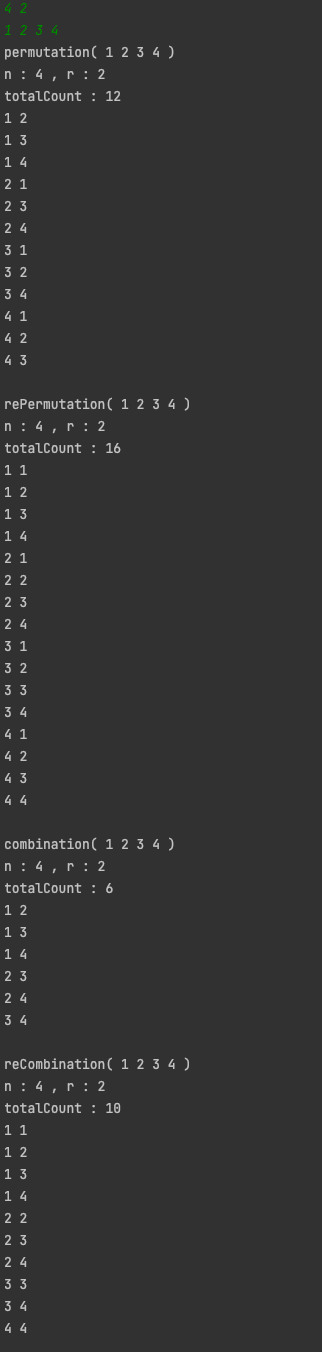
결과

백준 N과 M ( 1 ~ 4 )문제가 순서대로 순열, 조합, 중복순열, 중복 조합 문제
(검증하기 좋다 ㅎㅎ)

순열
- 중복 순열
조합
중복 조합
전체 소스
- 결과