Ian's Archive 🏃🏻

백준 이분 탐색 문제를 풀다 Parametric Search에 대해 알게 되었고, 정리 할 필요성을 느껴서 포스팅한다.

일단 이분탐색은 탐색 기법으로 원하는 탐색 범위를 두 부분으로 분할해서 찾는 방식이다
-> O(logN)의 시간 복잡도를 가지고 있다.

파라매트릭 서치는 최적화 문제 -> 결정문제로 바꾸어 푸는 것을 말한다.
(문제 상황을 만족하는 특정한 값 - 최소값, 최대값)

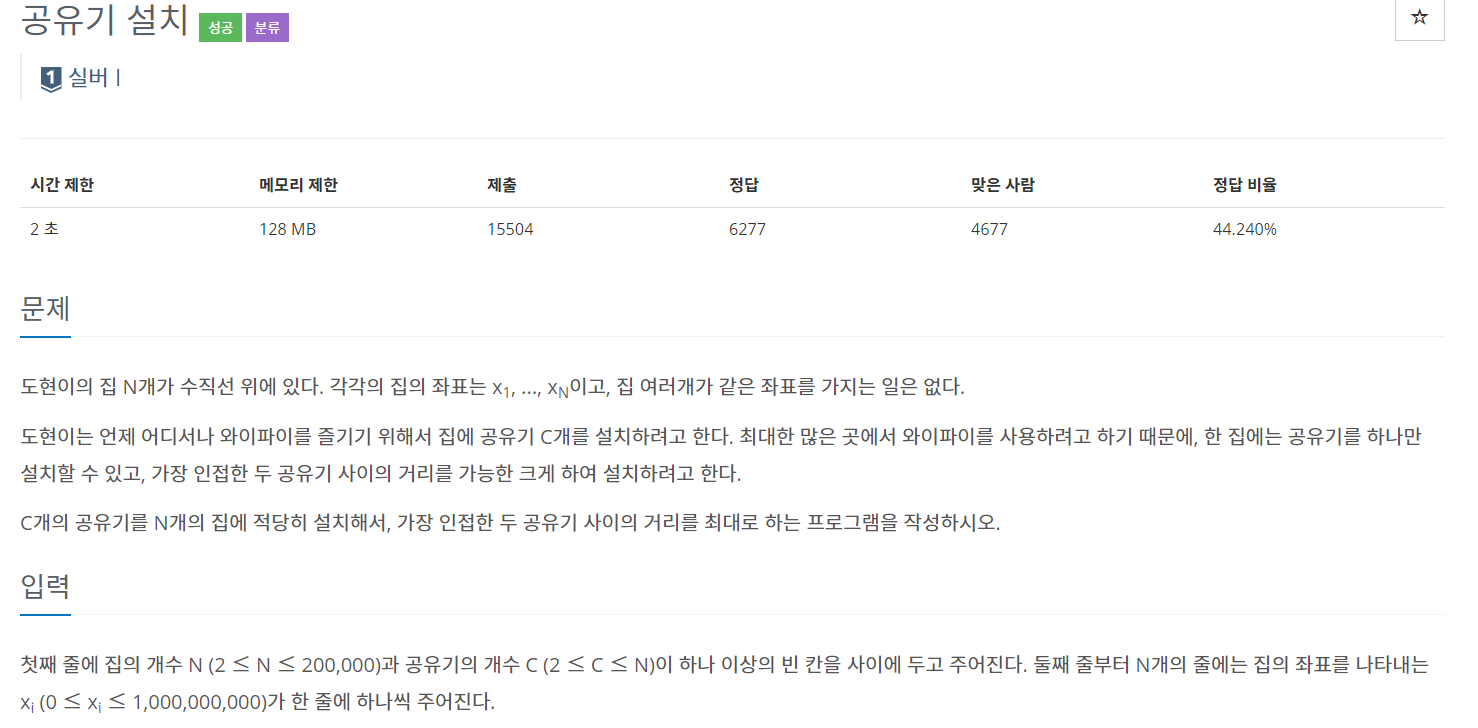
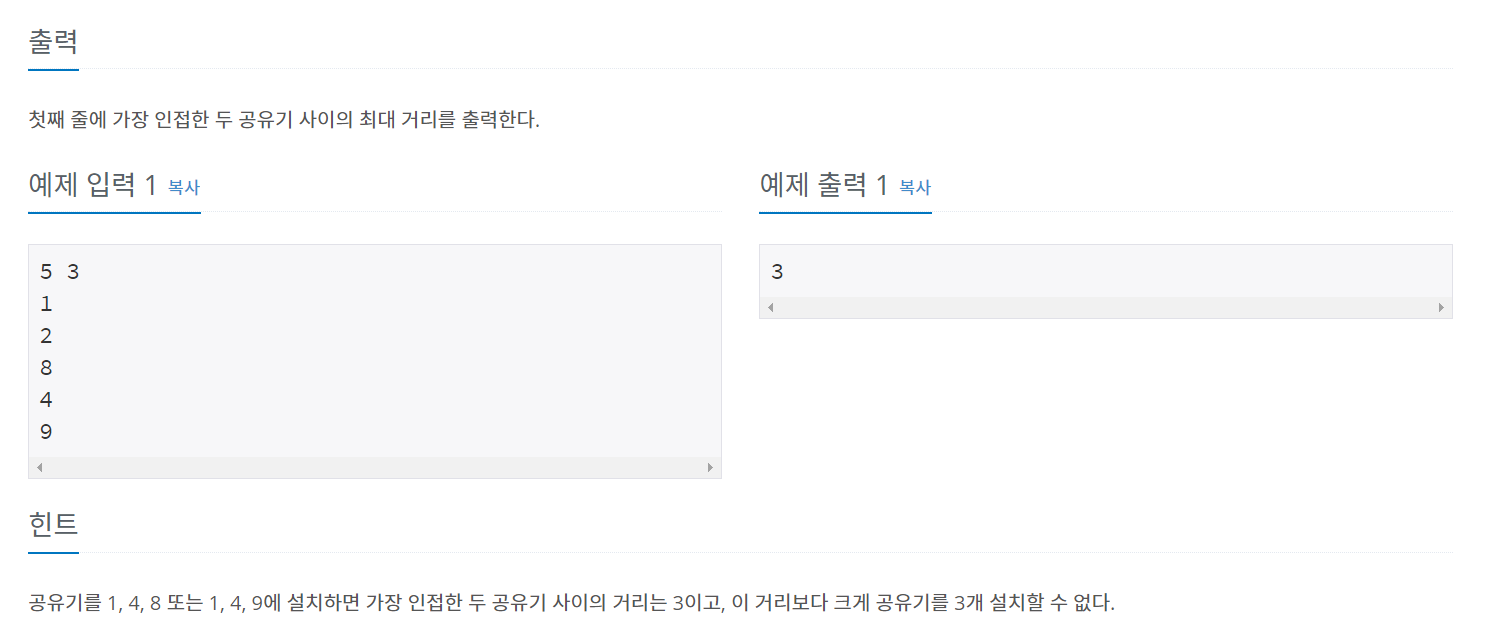
백준 2110번 문제가 쉽게 이해하기 좋은 문제인 것 같다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;

public class Main {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		String[] inputNK = br.readLine().split(" ");
		int N = Integer.parseInt(inputNK[0]);
		long K = Long.parseLong(inputNK[1]);
		long max = 0;

		long[] houseArr = new long[N];

		for(int i=0; i<N; i++) {
			houseArr[i] = Long.parseLong(br.readLine());
			max = max > houseArr[i] ? max : houseArr[i];
		}
		Arrays.sort(houseArr);

		max = Psearch(houseArr, K, max);
		System.out.println(max);
	}

	public static long Psearch(long[] houseArr, long K, long max) {
		long start = 1;
		long end = max;
		long ans = 0;

		while(start<=end) {
			long mid = (start+end)/2;

			if(checkHouse(houseArr, mid, K)) {
				start = mid+1;
				ans = ans > mid ? ans : mid;
			}else {
				end = mid-1;
			}
		}
		return ans;
	}

	public static boolean checkHouse(long[] houseArr, long mid, long K) {
		long temp = houseArr[0];
		long index = 0;
		for(int i = 1; i<houseArr.length; i++) {
			if(houseArr[i]-temp >= mid) {
				index++;
				temp=houseArr[i];
			}
		}

		if(index >=K-1)
			return true;
		else
			return false;
	}

}

이 문제의 포인트는

1. 공유기 사이 거리를 정한 후, 정한 거리 이상의 간격으로 집에 설치 가능한지 확인
   • 설치 가능 -> 더 큰 거리값 확인
   • 설치 불가능 -> 작은 거리값을 확인

추가로 백준 12015번 문제를 풀어보는 것을 추천한다. dp를 활용해 가장 긴 증가하는 부분 수열 구할 수 있는데 이분탐색을 사용하면 O(logN)으로 구할 수 있다.